Young’s lattice and the RSK algorithm

This section provides some examples on Young’s lattice and the RSK (Robinson-Schensted-Knuth) algorithm explained in Chapter 8 of Stanley’s book [Stanley2013].

Young’s Lattice

We begin by creating the first few levels of Young’s lattice \(Y\). For this, we need to define the elements and the order relation for the poset, which is containment of partitions:

sage: level = 6
sage: elements = [b for n in range(level) for b in Partitions(n)]
sage: ord = lambda x,y: y.contains(x)
sage: Y = Poset((elements,ord), facade=True)
sage: H = Y.hasse_diagram()

The resulting image looks best when dot2tex is installed:

sage: view(H)  # not tested

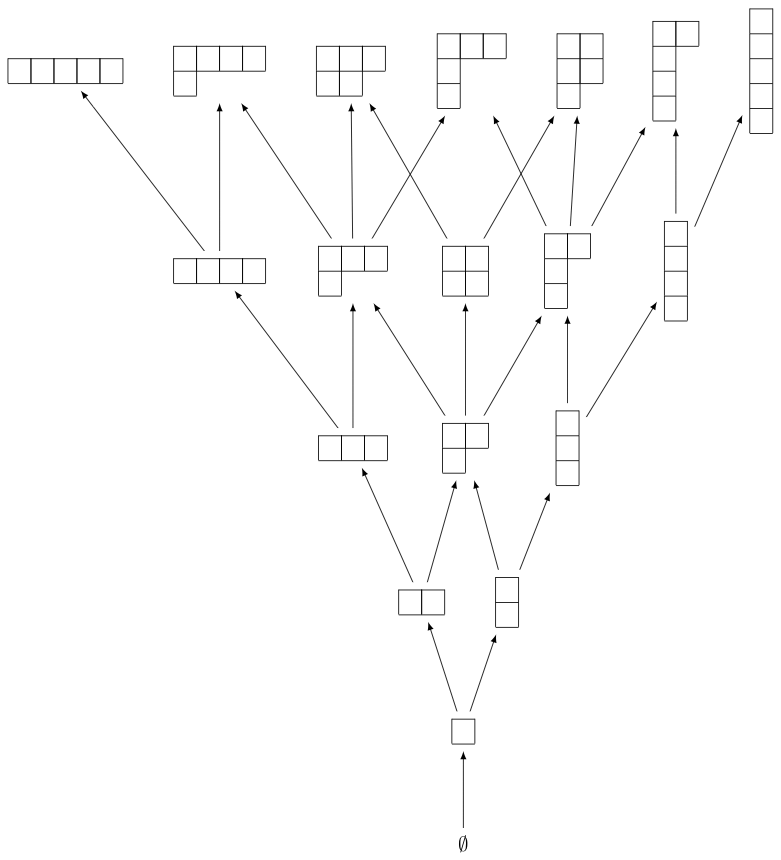
We can now define the up and down operators \(U\) and \(D\) on \(\QQ Y\). First we do so on partitions, which form a basis for \(\QQ Y\):

sage: QQY = CombinatorialFreeModule(QQ,elements)

sage: def U_on_basis(la):
....:     covers = Y.upper_covers(la)
....:     return QQY.sum_of_monomials(covers)

sage: def D_on_basis(la):
....:     covers = Y.lower_covers(la)
....:     return QQY.sum_of_monomials(covers)

As a shorthand, one also can write the above as:

sage: U_on_basis = QQY.sum_of_monomials * Y.upper_covers
sage: D_on_basis = QQY.sum_of_monomials * Y.lower_covers

Here is the result when we apply the operators to the partition \((2,1)\):

sage: la = Partition([2,1])
sage: U_on_basis(la)
B[[2, 1, 1]] + B[[2, 2]] + B[[3, 1]]
sage: D_on_basis(la)
B[[1, 1]] + B[[2]]

Now we define the up and down operator on \(\QQ Y\):

sage: U = QQY.module_morphism(U_on_basis)
sage: D = QQY.module_morphism(D_on_basis)

We can check the identity \(D_{i+1} U_i - U_{i-1} D_i = I_i\) explicitly on all partitions of \(i=3\):

sage: for p in Partitions(3):
....:     b = QQY(p)
....:     assert D(U(b)) - U(D(b)) == b

We can also check that the coefficient of \(\lambda \vdash n\) in \(U^n(\emptyset)\) is equal to the number of standard Young tableaux of shape \(\lambda\):

sage: u = QQY(Partition([]))
sage: for i in range(4):
....:     u = U(u)
sage: u
B[[1, 1, 1, 1]] + 3*B[[2, 1, 1]] + 2*B[[2, 2]] + 3*B[[3, 1]] + B[[4]]

For example, the number of standard Young tableaux of shape \((2,1,1)\) is \(3\):

sage: StandardTableaux([2,1,1]).cardinality()
3

We can test this in general:

sage: for la in u.support():
....:     assert u[la] == StandardTableaux(la).cardinality()

We can also check this against the hook length formula (Theorem 8.1):

sage: def hook_length_formula(p):
....:     n = p.size()
....:     return factorial(n) // prod(p.hook_length(*c) for c in p.cells())

sage: for la in u.support():
....:     assert u[la] == hook_length_formula(la)

RSK Algorithm

Let us now turn to the RSK algorithm. We can verify Example 8.12 as follows:

sage: p = Permutation([4,2,7,3,6,1,5])
sage: RSK(p)
[[[1, 3, 5], [2, 6], [4, 7]], [[1, 3, 5], [2, 4], [6, 7]]]

The tableaux can also be displayed as tableaux:

sage: P,Q = RSK(p)
sage: P.pp()
1  3  5
2  6
4  7
sage: Q.pp()
1  3  5
2  4
6  7

The inverse RSK algorithm is implemented as follows:

sage: RSK_inverse(P,Q, output='permutation')
[4, 2, 7, 3, 6, 1, 5]

We can verify that the RSK algorithm is a bijection:

sage: def check_RSK(n):
....:     for p in Permutations(n):
....:          assert RSK_inverse(*RSK(p), output='permutation') == p
sage: for n in range(5):
....:     check_RSK(n)